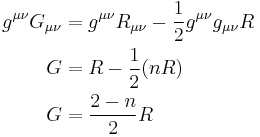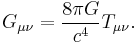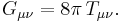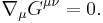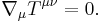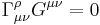Einstein tensor
In differential geometry, the Einstein tensor (also trace-reversed Ricci tensor), named after Albert Einstein, is used to express the curvature of a Riemannian manifold. In general relativity, the Einstein tensor occurs in the Einstein field equations for gravitation describing spacetime curvature in a manner consistent with energy considerations.
Contents |
Definition
The Einstein tensor  is a rank 2 tensor defined over Riemannian manifolds. In index-free notation it is defined as
is a rank 2 tensor defined over Riemannian manifolds. In index-free notation it is defined as
where  is the Ricci tensor,
is the Ricci tensor, 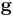 is the metric tensor and
is the metric tensor and  is the scalar curvature. In component form, the previous equation reads as
is the scalar curvature. In component form, the previous equation reads as
The Einstein tensor is symmetric
and, like the stress-energy tensor, divergenceless
Explicit form
The Ricci tensor depends only on the metric tensor, so the Einstein tensor can be defined directly with just the metric tensor. However, this expression is complex and rarely quoted in textbooks. The complexity of this expression can be shown using the formula for the Ricci tensor in terms of Christoffel symbols:
where 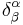 is the Kronecker tensor and the Christoffel symbol
is the Kronecker tensor and the Christoffel symbol 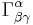 is defined as
is defined as
Before cancellations, this formula results in 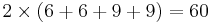 individual terms. Cancellations bring this number down somewhat.
individual terms. Cancellations bring this number down somewhat.
In the special case of a locally inertial reference frame near a point, the first derivatives of the metric tensor vanish and the component form of the Einstein tensor is considerably simplified:
where square brackets conventionally denote antisymmetrization over bracketed indices, i.e.
Trace
The trace of the Einstein tensor can be computed by contracting the equation in the definition with the metric tensor 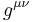 . In
. In  dimensions (of arbitrary signature):
dimensions (of arbitrary signature):
The special case of 4 dimensions in physics (3 space, 1 time) gives  , the trace of the Einstein tensor, as the negative of
, the trace of the Einstein tensor, as the negative of 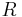 , the Ricci tensor's trace. Thus another name for the Einstein tensor is the trace-reversed Ricci tensor.
, the Ricci tensor's trace. Thus another name for the Einstein tensor is the trace-reversed Ricci tensor.
Use in general relativity
The Einstein tensor allows the Einstein field equations (without a cosmological constant) to be written in the concise form:
which becomes in geometrized units,
From the explicit form of the Einstein tensor, the Einstein tensor is a nonlinear function of the metric tensor, but is linear in the second partial derivatives of the metric. As a symmetric 2nd rank tensor, the Einstein tensor has 10 independent components in a 4-dimensional space. It follows that the Einstein field equations are a set of 10 quasilinear second-order partial differential equations for the metric tensor.
The Bianchi identities can also be easily expressed with the aid of the Einstein tensor:
The Bianchi identities automatically ensure the conservation of the stress-energy tensor in curved spacetimes:
The geometric significance of the Einstein tensor is highlighted by this identity. In coordinate frames respecting the gauge condition
an exact conservation law for the stress tensor density can be stated:
-
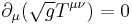 .
.
The Einstein tensor plays the role of distinguishing these frames.
See also
References
- Ohanian, Hans C.; Remo Ruffini (1994). Gravitation and Spacetime (Second edition ed.). W. W. Norton & Company. ISBN 0-393-96501-5.
- Martin, John Legat (1995). General Relativity: A First Course for Physicists. Prentice Hall International Series in Physics and Applied Physics (Revised edition ed.). Prentice Hall. ISBN 0-13-291196-5.
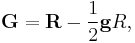
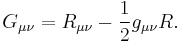
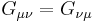
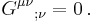
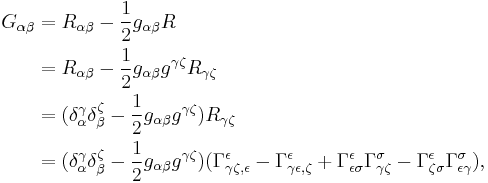
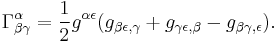
![\begin{align}G_{\alpha\beta} & = g^{\gamma\mu}\bigl[ g_{\gamma[\beta,\mu]\alpha} %2B g_{\alpha[\mu,\beta]\gamma} - \frac{1}{2} g_{\alpha\beta} g^{\epsilon\sigma} (g_{\epsilon[\mu,\sigma]\gamma} %2B g_{\gamma[\sigma,\mu]\epsilon})\bigr] \\ & = g^{\gamma\mu} (\delta^\epsilon_\alpha \delta^\sigma_\beta - \frac{1}{2} g^{\epsilon\sigma}g_{\alpha\beta})(g_{\epsilon[\mu,\sigma]\gamma} %2B g_{\gamma[\sigma,\mu]\epsilon}),\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/82d282358db7d6ad00c944aa613c86b3.png)
![g_{\alpha[\beta,\gamma]\epsilon} \, = \frac{1}{2} (g_{\alpha\beta,\gamma\epsilon} - g_{\alpha\gamma,\beta\epsilon}).](/2012-wikipedia_en_all_nopic_01_2012/I/df23c935a1c04f0d70766875f281a06b.png)